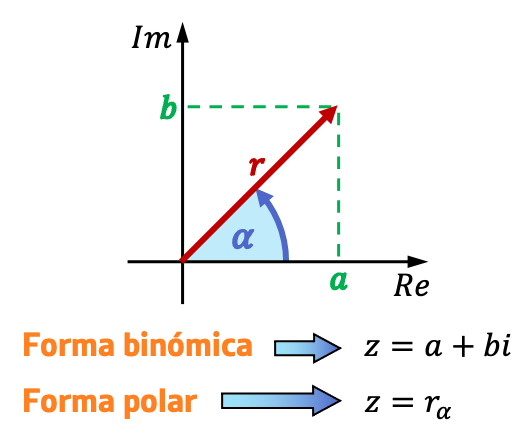
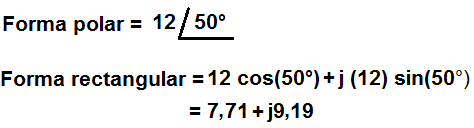Forma Rectangular de los Números Complejos
La forma rectangular de un número complejo es aquella que se expresa como Z = a + bi; Donde “a” es la parte real y “bi” es la parte imaginaria. Esta forma se puede visualizar como un vector en un plano cartesiano, donde “a” se ubica en el eje horizontal (eje real) y “b” en el eje vertical (eje imaginario).
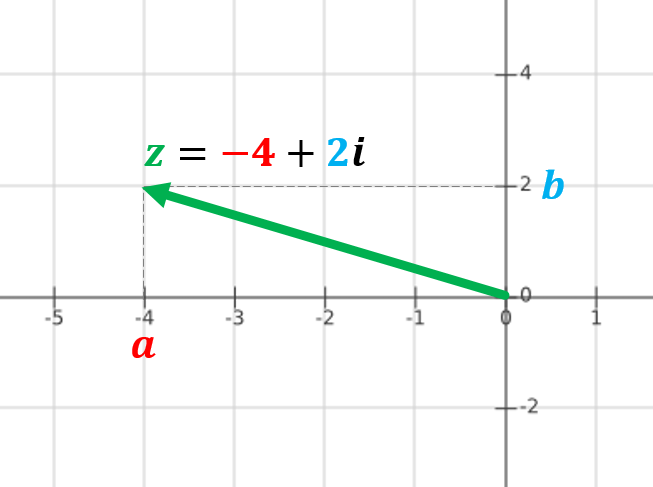
Figura 2. Los números complejos. Tomado de Mi Profe [Imagen] Mi Profe.com, 2025, https://miprofe.com/numeros-complejos/