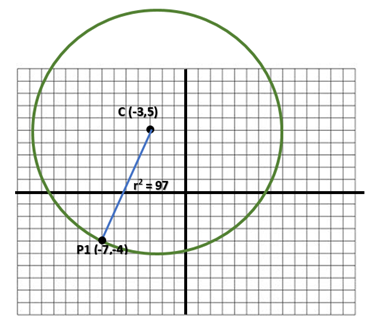
Primer ejemplo
Determina la ecuación de la circunferencia que tiene como radio el segmento AC donde C es el centro y tienen coordenadas; A (5, 6) y C (7 , -2)
Solución: Tal como se explicó anteriormente, solo tenemos que sustituir en la fórmula: (x – h)2 + (y –k)2 = (x1 – h)2 + (y1 – k)2
Sustituimos los valores del centro (h,k) y del punto A (X1,Y1) y nos queda: (x – 7)2 + (y + 2)2 = (5 – 7)2 + (6 + 2)2
Resolvemos y nos queda: X2 – 14x + 49 + y2 + 4y + 4 = 4 + 64
Acomodamos y despejamos para igualar a cero y obtener la forma general
x2 + y2 - 14x + 4y - 15 = 0
Ahora solo resta hacer la gráfica correspondiente, para ello graficamos el centro de la circunferencia y con un compás abierto a 7 unidades trazamos la circunferencia
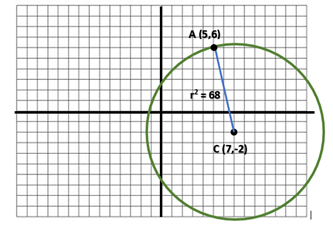
Fuente: Elaboración propia