Saltar la navegación

Ejemplos

Primer ejemplo

Tres sogas están atadas a una estaca y sobre ella actúan 3 fuerzas: F1 = 45N, F2 = 65N a 30° y F3 = 85N a -52° tal como se muestra en la figura

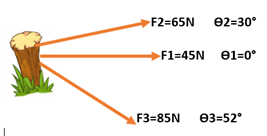
suma vectores2

Fuente: elaboración propia

Determina la fuerza resultante

Paso 1: Obtener las componentes

Utilizaremos la tabla que se vio en la explicación

Componente x (F)(cos θ) Componente y (F)(sen θ)
F1=45N    θ1= 0° 45 0
F2=65N   θ2=30° 56.29 32.5
F3=85N   θ3= -52° 52.33 -66.98

Tabla de elaboración propia

Paso 2: obtener las sumatorias

Incrementamos una fila al final para realizar las sumatorias

Componente x (F)(cos θ) Componente y (F)(sen θ)
F1=45N    θ1= 0° 45 0
F2=65N   θ2=30° 56.29 32.5
F3=85N   θ3= -52° 52.33 -66.98

∑Fx = 153.62N

 ∑Fy = -34.48N

Tabla de elaboración propia

Paso 3: calcular la magnitud de la fuerza resultante

Se utiliza el teorema de Pitágoras

FR = √ (156.622 + (-34.48)2) = 160.37N

Paso 4: se calcula el ángulo de inclinación

Utilizamos la función tangente:

θ = tan -1 ( -34.48/156.62) = -12,41°

POR TANTO LA FUERZA RESULTANTE DEL PROBLEMA ES:

FR = 160.37N    θ = -12.41°