Un Circuito Lógico es aquel que maneja la información en forma de "1" y "0", dos niveles lógicos de voltaje fijos, "1" nivel alto y "0" nivel bajo. Puede ser cualquier circuito que se comporte de acuerdo con un conjunto de reglas lógicas. Los circuitos lógicos, forman la base de cualquier dispositivo en el que se tengan que seleccionar o combinar señales de manera controlada.

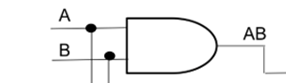
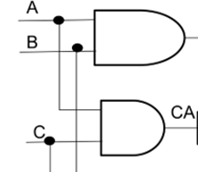
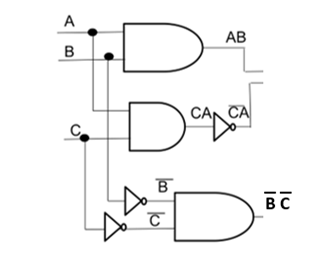
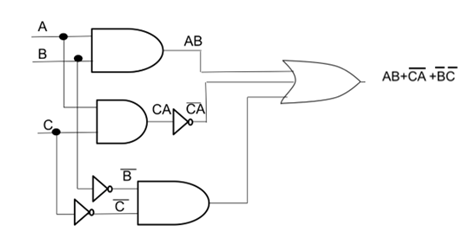
Los Circuitos Lógicos están compuestos por elementos digitales como la compuerta AND, compuerta OR, compuerta NOT y otras combinaciones muy complejas de los circuitos antes mencionados, aquí presentamos un ejemplo:

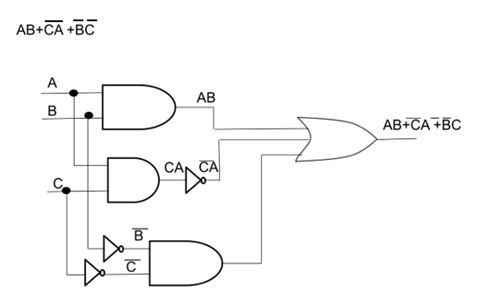
En esta imagen se puede apreciar que para cada diagrama corresponde una ecuación y viceversa, para cada ecuación corresponde un diagrama. En este subtema vamos a analizar como definir la ecuación booleana de un circuito a partir del diagrama

Para determinar la ecuación booleana a partir del dibujo del circuito debemos ir analizando a partir de cada una de las salidas y después de cada una de cada compuerta hasta llegar al final. De la forma que se presenta en el ejemplo, es decir, si realizamos un primer análisis podemos observar que se tienen tres entradas A, B y C, también tres compuertas AND de dos entradas, una compuerta OR de tres entradas y tres compuertas NOT. 

Vamos a analizar compuerta por compuerta de izquierda a derecha partiendo de las entradas, primero tenemos una compuerta AND a la que entran A y B, por lo que su salida será AB:

Luego tenemos otra compuerta AND, en la que entran A y C, por lo que su salida será AC o CA el orden no altera la compuerta:

Continuando con el análisis, se puede apreciar que saliendo de la segunda compuerta AND, se encuentra una compuerta NOR o inversor, lo que indica que se tendría la multiplicación CA negada o invertida es decir:

se tiene otra compuerta AND, en la que entran B y C  pero antes de entrar en la compuerta cada una de las entradas llega a un inversor (NOT), por lo que B y C

Y para terminar con el análisis de este circuito se tiene una compuerta OR de tres entradas que se alimenta de la salida de las tres compuertas AND previamente observadas, es decir:

Y de esta forma se obtiene la ecuación booleana a partir del diagrama del circuito