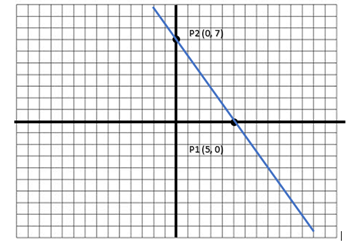
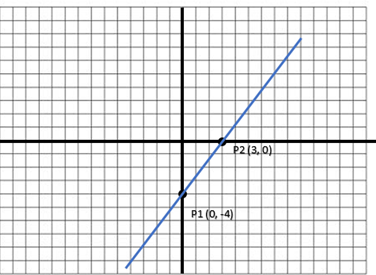
Cuando se trata de resolver problemas de Ecuación Simétrica de la recta, primero debemos entender que el problema nos debe proporcionar las coordenadas de los puntos de intersección con le ejes P1(a,0) y P2(0,b), con estos valores de a y b, sustituimos en la Ecuación general:
x/a + y/b = 1
y acomodamos los términos para que quede la forma:
Ax + By + C = 0
Encontrar la ecuación de la recta si cruza a los ejes coordenados en los siguientes puntos: P1(5,0) y P2(0,7)
Solución:
De la información que nos da el problema identificamos que a=5 y b=7
Ahora sustituimos estos valores en la ecuación: x/5 + y/7 = 1
Luego multiplicamos por 5 y por 7 para acomodar de la forma Ax + By + C = 0 y nos queda:
7x + 5y -35 = 0
Ahora solo falta hacer la gráfica correspondiente:
Fuente: Elaboración propia
Encontrar la ecuación de la recta si cruza a los ejes coordenados en los siguientes puntos P1(0, -4) y P2(3, -0):
Solución:
De la información que nos da el problema identificamos que a=3 y b=-4
Ahora sustituimos estos valores en la ecuación: x/3 + y/-4 = 1
Luego multiplicamos por 3 y por -4 para acomodar de la forma Ax + By + C = 0 y nos queda:
-4x + 3y + 12 = 0
Ahora solo falta hacer la gráfica correspondiente:
Fuente: Elaboración propia
Obra publicada con Licencia Creative Commons Reconocimiento Compartir igual 4.0