Para determinar la ecuación de una CIRCUNFERENCIA es necesario conocer las coordenadas del centro C(h,k) y la longitud del radio (r), con estos datos se aplica la fórmula general que es la siguiente:

(x - h)² + (y - k)² = r²   donde;

• (h, k) son las coordenadas del centro de la circunferencia
  
• r es la longitud del radio de la circunferencia

En este caso hablamos de que solo se conocen el centro y la ecuación de una recta que es tangente a la circunferencia, primero debemos tener claro que el radio formado por el centro y el punto tangente y la recta son perpendiculares entre sí, lo que nos remite a la fórmula de distancia de un punto a una recta: 

 Por lo tanto, esta fórmula la vamos a utilizar para obtener el radio: 

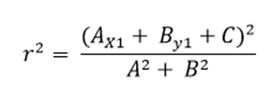 Ahora si esta fórmula para el radio la incorporamos dentro de la ecuación ordinario obtenemos: 

Que es la fórmula que vamos a utilizar para resolver los problemas